Zero-knowledge gouvernance 2026 : l’expression ne décrit plus seulement une confidentialité “sans clé côté fournisseur”. Désormais, elle engage une gouvernance cryptographique complète : plancher cryptographique non négociable, résistance au downgrade, négociation des paramètres KDF (PBKDF2, Argon2), entropie matérielle (hardware-rooted entropy) fondée sur une évaluation shannonienne de l’incertitude, et agilité cryptographique dans un monde post-quantique. Par conséquent, cette chronique clarifie la polysémie du terme et propose un cadre doctrinal, fondé sur des standards publics, sans posture polémique.
Résumé exécutif — Zero-knowledge gouvernance 2026
Constat
Le terme zero-knowledge s’est dilué. D’un côté, il renvoie aux Zero-Knowledge Proofs (ZKP) issus de la cryptographie académique. De l’autre, il désigne un modèle de chiffrement côté client où le fournisseur ne détient pas la clé. Cependant, ces deux acceptions restent conceptuellement distinctes.
Thèse doctrinale
En 2026, la question déterminante n’est plus seulement « le fournisseur voit-il la clé ? ». Désormais, on doit demander : « qui contrôle les paramètres cryptographiques et les chemins de négociation descendante ? » Ainsi, la discussion bascule vers la souveraineté des paramètres cryptographiques.
Ce que cette chronique apporte
Elle clarifie la différence entre ZKP et zero-knowledge encryption model. Ensuite, elle explicite pourquoi la gouvernance des paramètres KDF (itérations, mémoire, sel) définit un plancher cryptographique. Enfin, elle introduit deux pivots souvent absents : l’entropie matérielle et la gouvernance du cycle de vie des clés.
Angle moderne
La négociation descendante (downgrade) devient un angle doctrinal central : même si la clé reste côté client, un protocole tolérant des paramètres affaiblis peut réduire la robustesse effective sous certaines hypothèses de menace.
Point essentiel
Le zero-knowledge ne devient pas plus “vrai” parce qu’un éditeur l’affirme. En revanche, il devient plus robuste lorsque l’architecture impose un plancher cryptographique non négociable, documente les paramètres, verrouille les chemins de downgrade et explicite l’origine de l’entropie. Autrement dit, la maturité ne se mesure plus au slogan, mais à la gouvernance.
Note technique
Temps de lecture (express) : ~1 minutes
Temps de lecture (avancé) : ~2 minutes
Temps de lecture complet : ~50 minutes
Date de publication : 2026-02-21
Niveau : Cryptographie / Gouvernance / Architecture
Posture : Clarification doctrinale & gouvernance cryptographique
Catégorie : Digital Security
Langues disponibles : FR · EN (à venir)
Niveau d’impact : élevé (invariance paramétrique & modèle de confiance)
Cette chronique n’évalue aucun fournisseur en particulier. Elle propose un cadre conceptuel pour qualifier l’usage du terme zero-knowledge à l’ère de la gouvernance cryptographique et l’émergence cryptographique. Cela s’inscrit dans la continuité de la déclaration de transparence de l’IA de de Freemindtronic (Andorre) — AI-2025-11-SMD5
Cartographie conceptuelle : le terme zero-knowledge recouvre en 2026 trois réalités distinctes — propriété de preuve (ZKP), modèle de chiffrement côté client, et régime de gouvernance cryptographique. L’illustration suivante synthétise cette évolution doctrinale.
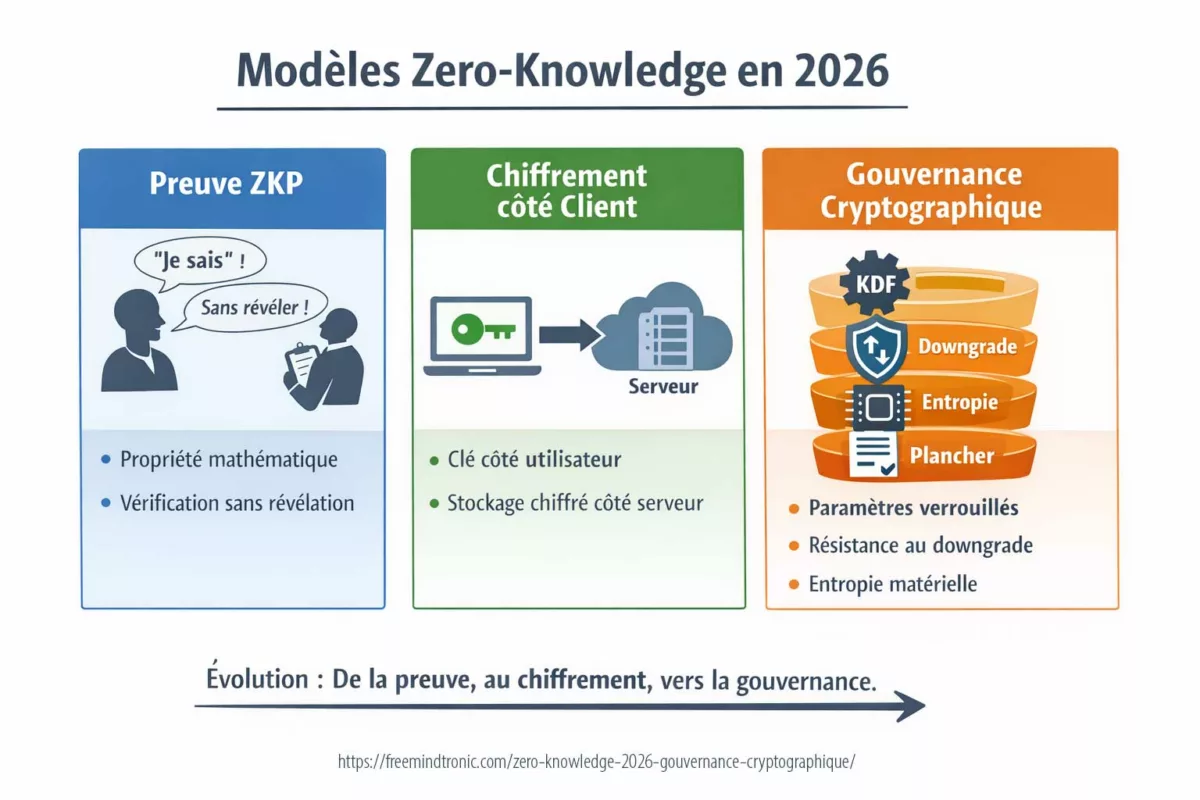
Cette chronique doctrinale appartient à la catégorie Digital Security. Elle prolonge le travail de clarification conceptuelle sur la souveraineté des paramètres cryptographiques et la robustesse des architectures zero-knowledge.
- Résumé exécutif
- Résumé avancé
- Chronique
- Dilution du terme
- Mutation doctrinale
- Origine académique (ZKP)
- Modèle de chiffrement côté client
- Limites contemporaines & downgrade
- Modèle de menace explicite
- Vérifiabilité du plancher
- Cycle de vie des clés (ISO 11770)
- Responsabilité cryptographique
- Agilité cryptographique
- Dimension quantique
- Entropie matérielle
- Cadre shannonien
- Comparatif entropie
- Zero-knowledge émergent
- Axiomes
- Principe d’émergence
- Formalisation mathématique
- Discussion critique
- Matrice de gouvernance
- Typologie analytique
- Limites & points d’arrêt
- Facteur humain
- Références officielles
- Bibliographie académique
- FAQ doctrinale
- Glossaire
- Définition stabilisée
- Perspective stratégique
Résumé avancé — De la promesse “sans clé” à la gouvernance cryptographique
⮞ Reading Note
Ce résumé avancé prend ~6 minutes. Il relie la sémantique du zero-knowledge aux standards publics, puis introduit la gouvernance des paramètres et les limites irréversibles.
D’abord, la cryptographie académique définit le zero-knowledge comme une propriété formelle de preuve. Ensuite, l’industrie a transposé le terme à des architectures de chiffrement côté client. Pourtant, cette transposition a créé une polysémie : on parle du même mot pour des objets conceptuels différents. Or, dès que la confiance repose sur une expression ambiguë, le débat se fragmente.
Ainsi, on doit qualifier le terme. Lorsque l’on parle de ZKP, on traite de vérification sans divulgation. En revanche, lorsque l’on parle de zero-knowledge encryption model, on traite de confidentialité des données, de possession de clé et de modèle de menace. Cependant, même dans ce second cas, la possession de clé ne suffit plus.
En 2026, la robustesse dépend fortement de la gouvernance des paramètres cryptographiques : choix du KDF, itérations, mémoire, parallélisme, sel, rétrocompatibilité. Par conséquent, une architecture peut rester “zero-knowledge” au sens de la clé, tout en devenant fragile au sens du plancher cryptographique si elle tolère des paramètres affaiblis ou des chemins de downgrade.
Le débat se déplace : au lieu de demander si un fournisseur “voit la clé”, on doit vérifier s’il contrôle — ou influence — les paramètres et les rétrocompatibilités qui définissent la résistance réelle.
Constat : dilution du terme et polysémie
Le terme zero-knowledge s’est diffusé parce qu’il résume une promesse intuitive : “le service ne peut pas lire”. Toutefois, cette promesse se décline en plusieurs mécanismes. D’une part, elle renvoie à des preuves cryptographiques formelles. D’autre part, elle renvoie à des systèmes de stockage chiffré. En conséquence, le débat mélange parfois preuve, chiffrement et gouvernance.
Pour éviter les affirmations absolues, on doit donc préciser l’objet : parle-t-on d’une preuve, d’un modèle de chiffrement, ou d’un régime de gouvernance des paramètres ? Cette chronique propose un cadre d’analyse, sans prétendre imposer une norme.
Mutation doctrinale : de propriété cryptographique à régime de gouvernance
Pendant plusieurs décennies, le zero-knowledge a désigné une propriété : une preuve sans divulgation. Ensuite, l’industrie a transposé le terme vers une architecture : le chiffrement côté client avec non-possession de clé.
Cependant, en 2026, une troisième étape apparaît. Le zero-knowledge devient un régime de gouvernance cryptographique.
Autrement dit, il ne décrit plus uniquement :
- Une propriété mathématique (ZKP),
- Ni un modèle technique (clé côté client),
Il décrit désormais :
- Un système de décision sur les paramètres,
- Un contrôle des planchers cryptographiques,
- Une gestion explicite des rétrocompatibilités,
- Une invariance paramétrique documentée.
Ainsi, le débat contemporain ne porte plus seulement sur la visibilité des secrets, mais sur l’autorité exercée sur les paramètres qui conditionnent leur robustesse.
En 2026, le zero-knowledge n’est plus seulement une propriété d’accès aux clés. Il devient un régime de gouvernance des paramètres cryptographiques et de leurs invariants.
Définition historique : origine académique du zero-knowledge (ZKP)
Les Zero-Knowledge Proofs (ZKP) décrivent une propriété où un vérificateur apprend uniquement la validité d’une assertion, sans obtenir d’information sur le secret. Goldwasser, Micali et Rackoff ont formalisé ce cadre et l’ont publié dans le Journal of the ACM. Ainsi, le “zero-knowledge” historique concerne un régime de preuve.
Référence académique : The Knowledge Complexity of Interactive Proof Systems (JACM).
Afin de clarifier la distinction entre la définition académique du Zero-Knowledge Proof (ZKP) et le modèle industriel de chiffrement zero-knowledge, le schéma suivant illustre le principe fondamental de vérification sans révélation du secret.
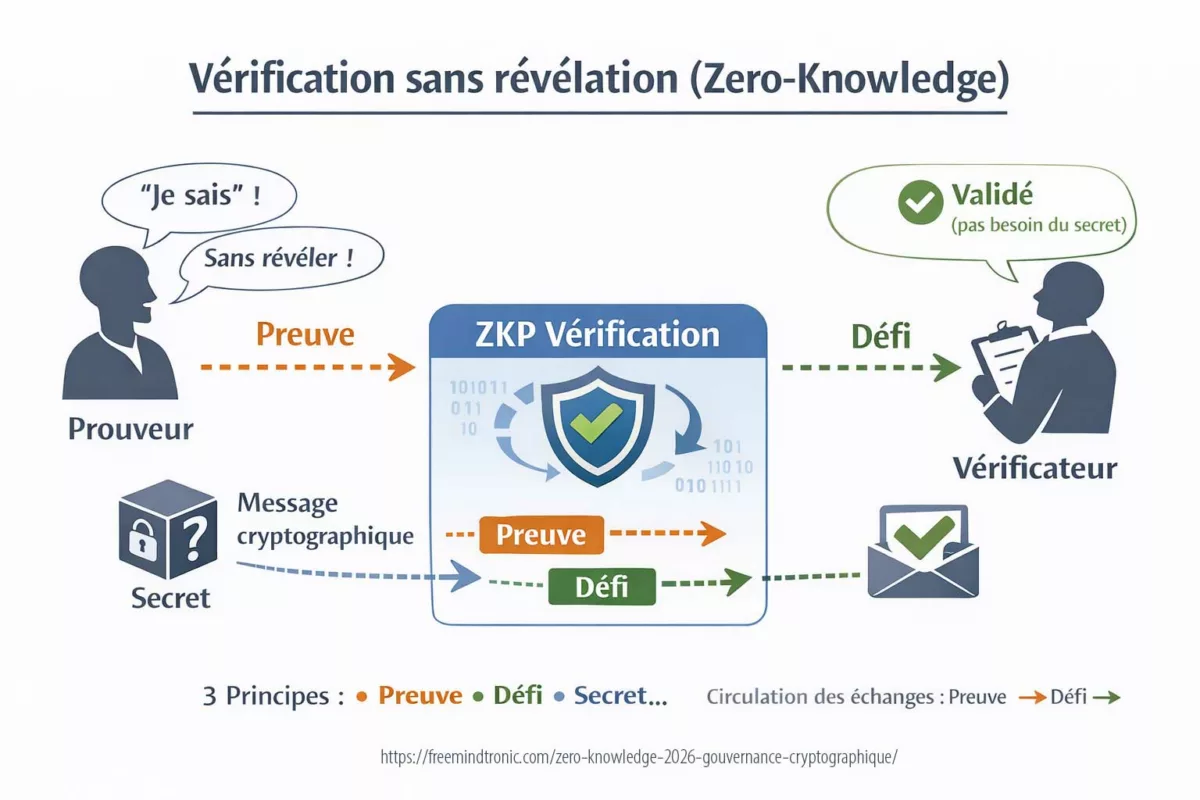
Définition opérationnelle : modèle zero-knowledge de chiffrement côté client
Dans son sens opérationnel, le zero-knowledge signifie généralement que le fournisseur ne détient pas la clé de déchiffrement. Par conséquent, le déchiffrement s’effectue côté client. Toutefois, cette définition suppose un modèle de menace souvent passif : le serveur stocke du chiffré, mais ne manipule pas activement les paramètres.
Or, en pratique, la dérivation de clé dépend de standards paramétrables. Ainsi, PBKDF2 et Argon2 définissent des réglages qui modifient directement la résistance au brute force. Références officielles :
Limites contemporaines : négociation KDF, rétrocompatibilité, downgrade
Lorsque l’architecture laisse le protocole négocier des paramètres (itérations, mémoire, modes hérités), elle crée un espace de gouvernance. Ainsi, un système peut préserver la non-possession de clé tout en tolérant des paramètres affaiblis pour des raisons de compatibilité. Par conséquent, on doit distinguer “confidentialité nominale” et “robustesse effective”.
Autrement dit, la question moderne devient : le client accepte-t-il une négociation descendante ? Si oui, alors le plancher cryptographique devient négociable. Or, une fois que des paramètres faibles ont servi à dériver une clé, la correction exige généralement re-dérivation et re-chiffrement : on ne “répare” pas rétroactivement la robustesse.
La résistance au downgrade cryptographique constitue aujourd’hui un critère déterminant de maturité zero-knowledge. Le schéma ci-dessous synthétise les trois piliers d’un plancher cryptographique non négociable : verrouillage, renforcement paramétrique et auditabilité.
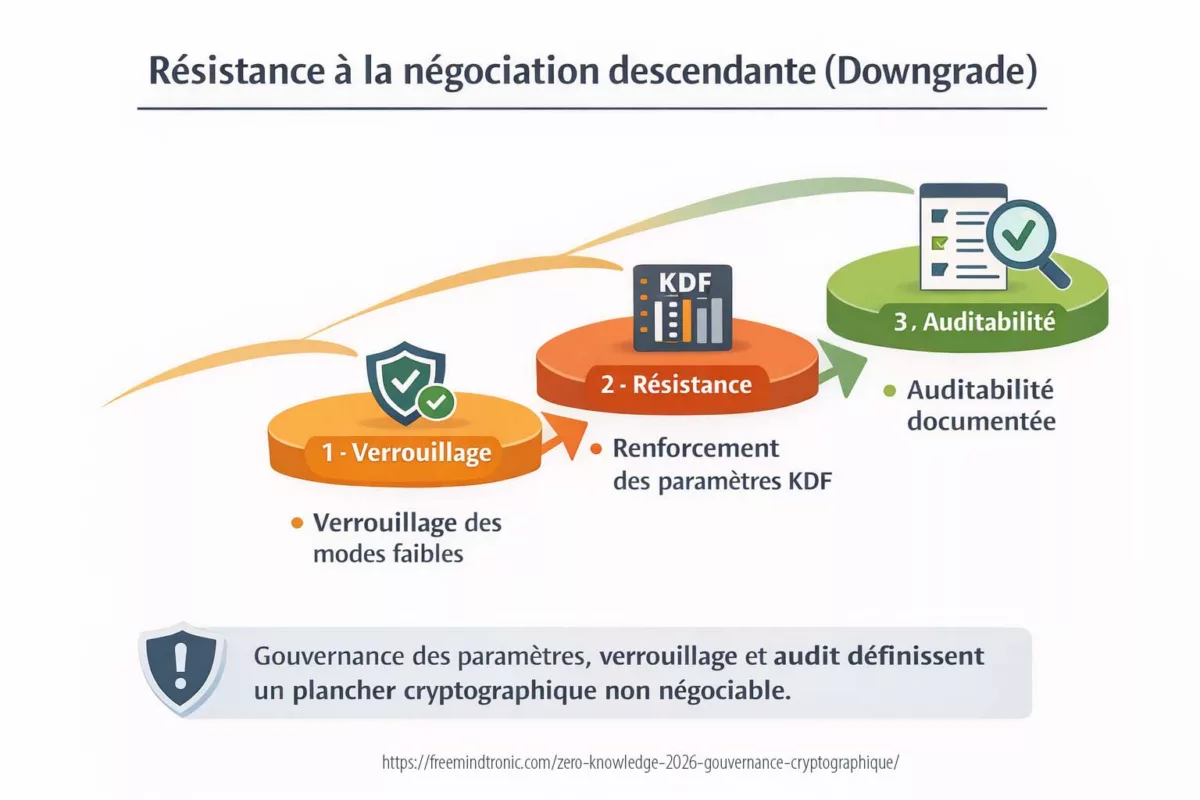
Modèle de menace explicite du zero-knowledge en 2026
Toute qualification du zero-knowledge suppose un modèle de menace clairement défini. En l’absence de cette explicitation, le terme risque de devenir purement déclaratif.
En 2026, plusieurs hypothèses d’attaque doivent être distinguées :
1 — Attaquant passif côté serveur
Le fournisseur stocke des données chiffrées sans chercher à influencer les paramètres. Dans ce modèle classique, la non-possession de clé constitue la condition principale.
2 — Attaquant actif négociateur
Le serveur ou un intermédiaire peut influencer la négociation des paramètres (KDF, algorithmes, rétrocompatibilités). Ici, la robustesse dépend de l’invariance paramétrique et de la résistance au downgrade.
3 — Attaquant matériel ou local
L’attaquant cible la mémoire volatile, les dispositifs physiques ou les segments autonomes. Dans ce cas, la volatilité stricte et l’autonomie entropique deviennent déterminantes.
4 — Attaquant à capacité étendue (post-quantique)
L’hypothèse d’un adversaire disposant de capacités computationnelles avancées impose une réflexion sur l’agilité cryptographique et la migration ascendante.
Ainsi, la gouvernance cryptographique consiste à aligner les paramètres, l’entropie et les mécanismes d’invariance sur les hypothèses d’attaque retenues.
ISO/IEC 11770 : gouvernance du cycle de vie des clés
Ensuite, la doctrine de sécurité doit intégrer la gestion du cycle de vie des clés : génération, distribution, stockage, révocation. ISO/IEC 11770 formalise ces mécanismes. Ainsi, la sécurité ne se limite pas à l’algorithme : elle dépend aussi des processus et des responsabilités.
Référence officielle : ISO/IEC 11770 — Key Management.
Responsabilité et imputabilité cryptographique
À mesure que le zero-knowledge devient une question de gouvernance, une interrogation supplémentaire apparaît : qui assume la responsabilité du plancher cryptographique ?
Les standards définissent des mécanismes. Cependant, ils ne désignent pas toujours clairement l’autorité décisionnelle sur les paramètres.
Or, dans une architecture zero-knowledge contemporaine :
- Quel acteur fixe le nombre minimal d’itérations ?
- Qui décide de supprimer un mode hérité ?
- Qui documente publiquement le plancher ?
- Qui engage sa responsabilité en cas de paramètre insuffisant ?
Ainsi, la gouvernance cryptographique devient une question d’imputabilité.
En effet, un plancher non documenté rend la responsabilité diffuse. À l’inverse, un plancher explicitement publié crée un engagement technique et éditorial.
Vérifiabilité du plancher cryptographique
Déclarer un plancher cryptographique ne suffit pas. Encore faut-il qu’il soit vérifiable.
La robustesse doctrinale du zero-knowledge dépend de la capacité d’un utilisateur, d’un auditeur ou d’un expert indépendant à constater :
- Les paramètres KDF effectivement utilisés (itérations, mémoire, parallélisme).
- L’absence de modes hérités activables.
- L’impossibilité technique d’un downgrade silencieux.
- La conformité aux standards publics annoncés.
Auditabilité
La vérifiabilité peut reposer sur :
- Une documentation publique des paramètres.
- Des audits indépendants.
- Une inspection du code lorsque cela est possible.
- Des mécanismes d’attestation ou de preuve de configuration.
Limite doctrinale
Un plancher non documenté ou non vérifiable reste une déclaration unilatérale.
En 2026, un zero-knowledge mature ne se contente pas d’affirmer la non-possession de clé. Il rend son plancher paramétrique observable et contrôlable.
La vérifiabilité devient ainsi un prolongement naturel de la gouvernance cryptographique.
Agilité cryptographique : perspective ENISA
Par ailleurs, la transition post-quantique réactive la notion d’agilité cryptographique. ENISA souligne l’intérêt d’architectures capables d’évoluer sans rupture systémique. Cependant, l’agilité ne justifie pas la permissivité au downgrade : elle organise la migration ascendante, pas la dégradation.
Référence ENISA : Post-Quantum Cryptography: current state and quantum mitigation.
Dimension quantique et gouvernance cryptographique
L’émergence des capacités de calcul quantique ne remet pas en cause l’ensemble de la cryptographie contemporaine. Elle affecte principalement certaines primitives asymétriques (RSA, ECC, Diffie–Hellman) via l’algorithme de Shor, ainsi que la recherche exhaustive via l’algorithme de Grover.
Impact différencié
Il convient de distinguer :
- Cryptographie asymétrique classique : vulnérable à long terme (Shor).
- Cryptographie symétrique bien dimensionnée : résistance réduite quadratiquement (Grover), mais conservant une sécurité exponentielle si les tailles de clés sont adaptées (ex. 256 bits).
- Fonctions mémoire-hard (Argon2) : dépendance au coût matériel et énergétique, moins favorable aux accélérations quantiques massives.
Ainsi, le risque quantique impose une gouvernance adaptative des paramètres, mais ne rend pas obsolètes les architectures symétriques correctement dimensionnées.
Harvest now, decrypt later
Le risque stratégique majeur réside dans la capture actuelle de données chiffrées destinées à être déchiffrées ultérieurement lorsque les capacités quantiques seront suffisantes.
Dans ce contexte :
- Les architectures à secret persistant sont structurellement exposées.
- Les architectures à clé émergente strictement volatile réduisent la surface de captation différée.
Une clé qui n’existe qu’au moment de l’usage, puis disparaît, limite mécaniquement l’intérêt d’une captation longue durée.
Conséquence doctrinale
En 2026, la maturité zero-knowledge implique :
- Une capacité de migration ascendante vers des primitives post-quantiques si nécessaire.
- Une augmentation anticipée des tailles de clés symétriques.
- Un refus des mécanismes asymétriques vulnérables à long terme.
- Une réduction structurelle des secrets persistants.
Le quantique ne redéfinit pas le zero-knowledge ; il renforce l’exigence de gouvernance paramétrique et de limitation ontologique des secrets durables.
Approfondissements techniques
Pour une analyse détaillée des vulnérabilités asymétriques face aux capacités quantiques émergentes : Quantum threats to encryption
Pour une étude spécifique de la robustesse d’AES-256, de la segmentation de clé et de la résilience face à Grover : AES-256 CBC quantum security & key segmentation
Analyse des implications du quantique sur RSA et les mécanismes asymétriques classiques : Quantum computing and RSA encryption
Pour un aperçu des avancées récentes en calcul quantique et de leur portée réelle en matière cryptographique : Quantum computer 6100 qubits – Historic 2025 breakthrough.
Entropie informationnelle et entropie matérielle — Fondement shannonien
La robustesse d’un système zero-knowledge ne dépend pas uniquement d’un algorithme, ni même d’un nombre d’itérations KDF. Elle dépend en amont d’un paramètre plus fondamental : l’entropie.
Pour une application concrète de cette limite entropique dans le contexte de l’ère quantique et des mots de passe à haute imprévisibilité, voir : How to create and protect strong passwords in the age of quantum computing.
Claude Shannon a défini l’entropie informationnelle comme mesure mathématique de l’incertitude d’une source. En cryptographie, cette incertitude conditionne directement la résistance aux attaques exhaustives. Autrement dit, un secret à faible entropie reste structurellement vulnérable, quel que soit l’algorithme employé.
Ainsi, dans une architecture zero-knowledge, l’entropie initiale devient une frontière irréversible. Si la génération de clé repose sur une source faiblement entropique, aucune augmentation ultérieure du nombre d’itérations, ni aucun ajustement paramétrique, ne peut restaurer l’imprévisibilité perdue.
Cette réalité rejoint les exigences des standards contemporains, notamment la série NIST SP 800-90 relative aux générateurs de bits aléatoires. Cependant, au-delà des implémentations techniques, le principe reste shannonien : la sécurité ne peut dépasser l’entropie de sa source.
Le plancher cryptographique réel d’un système zero-knowledge est borné par l’entropie effective à la génération des clés. Si cette entropie est insuffisante, la limite devient structurelle et irréversible.
Par conséquent, lorsqu’on analyse la gouvernance cryptographique zero-knowledge, il ne suffit pas de vérifier la non-possession de clé ou la résistance au downgrade. Il faut également examiner la qualité informationnelle de la source d’entropie.
Pourquoi un cadre shannonien plutôt qu’une simple “méthode d’entropie” ?
Lorsqu’une architecture affirme générer de l’entropie, elle peut se référer à des méthodes techniques concrètes : générateur pseudo-aléatoire, TRNG matériel, bruit thermique, oscillations physiques, etc. Toutefois, ces mécanismes décrivent une implémentation. Ils ne définissent pas, en eux-mêmes, un cadre théorique de mesure.
Claude Shannon, dans sa théorie mathématique de l’information (1948), a introduit une mesure formelle de l’incertitude : l’entropie informationnelle. Cette mesure ne dépend pas d’un dispositif particulier ; elle modélise le degré d’imprévisibilité d’une source.
En se référant à Shannon, une architecture ne revendique pas un procédé spécifique de génération d’aléa. Elle adopte un cadre d’évaluation : la sécurité effective ne peut excéder l’entropie mesurable du secret initial.
Ainsi, le choix d’un cadre shannonien ne remplace pas les standards techniques (NIST SP 800-90, ISO/IEC 11770, RFC 9106). Il les précède conceptuellement. Il rappelle que :
- Un secret de faible entropie reste vulnérable, même avec un algorithme robuste.
- Un nombre élevé d’itérations KDF n’augmente pas l’espace de clés si l’entropie initiale est bornée.
- La résistance exponentielle dépend directement du nombre effectif de bits d’incertitude.
Autrement dit, la référence à Shannon n’est pas un argument marketing. C’est un rappel mathématique : la sécurité cryptographique est plafonnée par l’entropie informationnelle du secret généré.
Dans cette perspective, la gouvernance cryptographique zero-knowledge doit examiner non seulement les algorithmes, mais aussi la qualité mesurable de la source d’incertitude. C’est pourquoi un cadre shannonien offre une base conceptuelle plus fondamentale qu’une simple description de méthode.
Entropie informationnelle : Shannon face aux méthodes de génération
Lorsqu’une architecture cryptographique affirme « générer de l’entropie », elle peut en réalité désigner des mécanismes très différents. Avant de comparer les approches, il convient de rappeler la base théorique.
1 — Le cadre fondamental : l’entropie selon Shannon (1948)
Claude Shannon a défini l’entropie informationnelle comme mesure mathématique de l’incertitude d’une variable aléatoire. Elle s’exprime par la formule :
Cette équation mesure le nombre moyen de bits d’incertitude d’une source. En cryptographie, cela signifie que la résistance théorique d’un secret dépend directement du nombre effectif de bits d’imprévisibilité.
Ainsi, si un secret possède 128 bits d’entropie réelle, sa résistance maximale correspond à un espace de 2¹²⁸ possibilités. En revanche, si l’entropie effective n’est que de 40 bits, l’espace réel n’est plus que de 2⁴⁰, indépendamment de l’algorithme utilisé.
2 — Méthodes courantes de génération d’entropie
En pratique, plusieurs mécanismes techniques sont utilisés pour produire de l’aléa :
- PRNG (Pseudo-Random Number Generator) : générateurs déterministes initialisés par une graine.
- DRBG conformes NIST SP 800-90A : générateurs déterministes sécurisés.
- TRNG (True Random Number Generator) : bruit thermique, oscillations électroniques, jitter.
- HRNG (Hardware Random Number Generator) : circuits dédiés intégrés aux processeurs.
- Sources environnementales : mouvements de souris, timings clavier, événements système.
Ces méthodes décrivent comment l’aléa est produit. Toutefois, elles ne répondent pas directement à la question fondamentale : quelle est l’entropie mesurable réellement obtenue ?
3 — Limites structurelles des approches purement techniques
Un PRNG, par définition, ne crée pas d’entropie ; il l’étend à partir d’une graine initiale. Si cette graine est faible, toute la séquence devient prédictible.
Un TRNG matériel peut produire un bruit physique robuste, mais il nécessite une validation statistique continue pour éviter les biais.
Les sources environnementales offrent souvent une entropie limitée et difficilement quantifiable.
Autrement dit, ces méthodes décrivent des mécanismes physiques ou logiciels. Elles ne constituent pas, en elles-mêmes, un cadre théorique de mesure de la sécurité.
4 — Pourquoi un cadre shannonien est plus pertinent doctrinalement
Se référer à Shannon ne signifie pas ignorer les méthodes techniques. Au contraire, cela impose une exigence supplémentaire : mesurer et borner l’entropie effective.
Le cadre shannonien permet :
- De quantifier l’incertitude réelle d’un secret.
- D’évaluer l’espace de recherche effectif d’un attaquant.
- D’identifier une limite théorique indépendante des implémentations.
- D’éviter la confusion entre « complexité algorithmique » et « imprévisibilité réelle ».
Ainsi, alors qu’une méthode technique décrit un processus, le cadre shannonien définit une borne mathématique. Il précède l’implémentation et structure son évaluation.
En conséquence, dans une analyse de gouvernance cryptographique zero-knowledge, la question pertinente devient :
Cette question dépasse la simple description d’un générateur. Elle engage la sécurité exponentielle du système.
Application pratique d’un cadre shannonien — Freemindtronic
Dans le cadre de ses architectures de sécurité, Freemindtronic a fait le choix méthodologique d’utiliser un référentiel shannonien pour évaluer l’entropie lors de la génération de clés, de mots de passe et de segments cryptographiques.
Ce choix ne concerne pas l’algorithme de chiffrement lui-même — lequel repose sur des standards ouverts — mais la manière dont l’incertitude initiale est mesurée et contrôlée au moment de la génération du secret.
Concrètement, l’objectif est d’estimer le nombre effectif de bits d’entropie informationnelle produits au moment de la création. Cette évaluation s’inscrit dans une logique mathématique : la sécurité maximale atteignable ne peut excéder l’entropie mesurable du secret généré.
Ainsi, plutôt que de se limiter à la description d’un générateur pseudo-aléatoire ou matériel, l’architecture adopte une approche fondée sur la quantification de l’incertitude selon la théorie de l’information.
Ce positionnement s’inscrit dans une continuité académique. Il ne constitue pas une rupture avec les standards techniques (NIST SP 800-90, ISO/IEC 11770, RFC 9106), mais une couche conceptuelle supplémentaire visant à encadrer la génération des secrets.
En conséquence, ce choix doctrinal vise à assurer une cohérence entre génération de secret, borne mathématique de sécurité et gouvernance cryptographique globale.
Zero-knowledge émergent non médié
Le système décrit dans le brevet WO2018154258A1 repose sur une segmentation de clé distribuée sur plusieurs dispositifs physiques NFC, avec reconstruction locale et stockage exclusivement volatile.
Contrairement à un schéma classique de partage de secret, aucun secret maître persistant n’est découpé. Chaque segment constitue une entité cryptographique autonome.
La clé effective n’existe pas en permanence. Elle émerge temporairement d’une composition locale volontaire, puis disparaît après usage.
Schéma synthétique : dans une architecture à clé segmentée, la clé opérationnelle n’est jamais stockée de manière persistante. Elle est reconstruite localement en mémoire volatile, par concaténation contrôlée de segments cryptographiques autonomes (ex. dispositifs NFC, clé USB, SSD), puis effacée immédiatement après usage. Aucun serveur, aucune base de données centrale, aucune clé maîtresse persistante n’existent dans l’architecture.
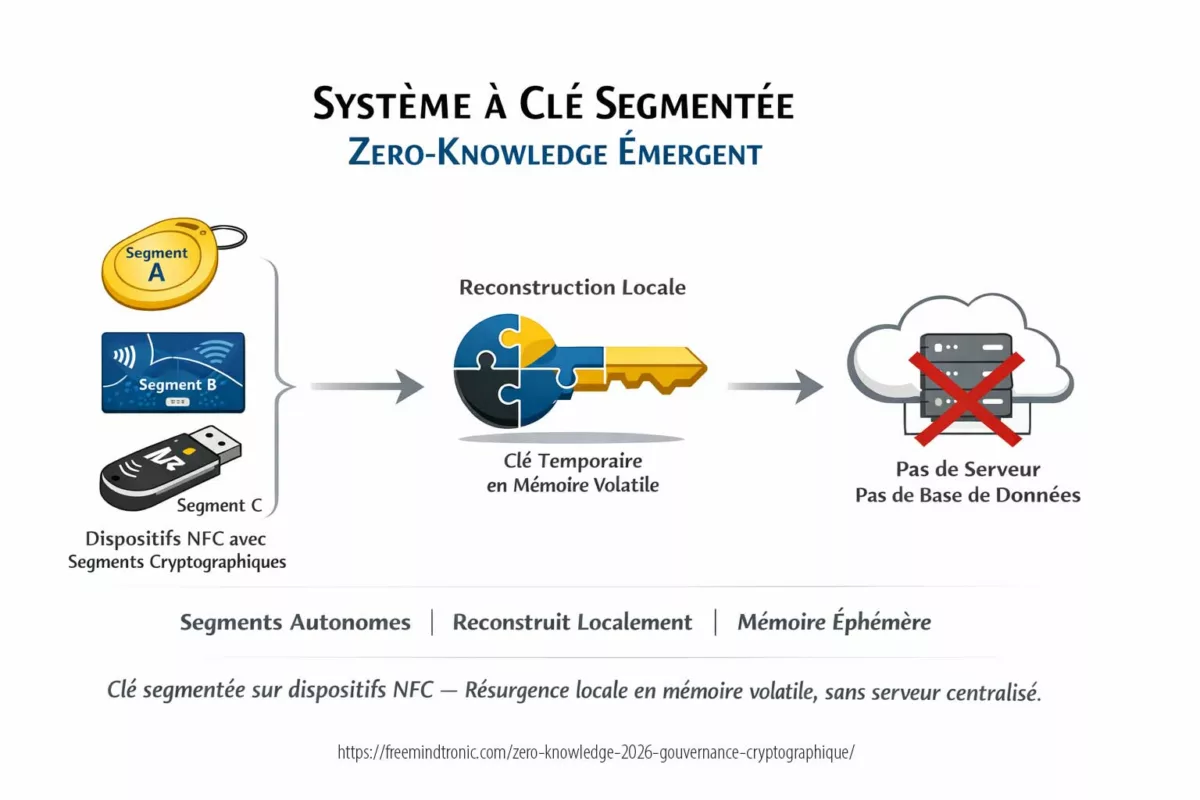
Cette architecture peut être qualifiée, au sens analytique, de « zero-knowledge émergent non médié ».
Elle ne repose pas sur la non-possession d’un tiers, mais sur l’inexistence structurelle de tout intermédiaire susceptible de détenir ou de négocier les paramètres.
La confidentialité découle donc d’une absence ontologique de médiation et d’une volatilité stricte de la clé effective.
5 — Intégration dans la matrice de gouvernance
Dans la matrice doctrinale, la dimension « entropie » doit donc être évaluée en termes shannoniens :
| Dimension | Question | Risque si faible | Irréversibilité |
|---|---|---|---|
| Entropie informationnelle | Nombre effectif de bits d’incertitude mesurable ? | Réduction exponentielle de l’espace de clés | Critique |
Une fois qu’un secret a été généré avec une entropie limitée, aucune augmentation ultérieure du nombre d’itérations KDF ni aucun changement d’algorithme ne peut restaurer rétroactivement l’incertitude perdue.
Par conséquent, le recours à Shannon ne relève pas d’un choix marketing ni d’une préférence technologique. Il s’agit d’un positionnement conceptuel : évaluer la sécurité à partir de sa limite informationnelle fondamentale.
Axiomes du zero-knowledge émergent
Afin de clarifier la nature spécifique d’une architecture à segments autonomes, on peut formuler quatre axiomes analytiques. Ces axiomes ne constituent pas une norme, mais un cadre de compréhension.
Axiome 1 — Inexistence persistante de la clé
La clé effective n’existe pas de manière durable. Elle apparaît uniquement lors de la composition volontaire des segments, puis disparaît après usage. Ainsi, il n’existe aucun secret central stocké en permanence.
Axiome 2 — Autonomie entropique des segments
Chaque segment possède une entropie propre et mesurable. La compromission d’un segment ne révèle ni la totalité de l’espace combinatoire ni les autres segments.
Axiome 3 — Composition locale non médiée
La reconstruction s’effectue localement, sans tiers intermédiaire, sans serveur et sans base de données centralisée. Par conséquent, aucune négociation distante des paramètres n’est possible.
Axiome 4 — Volatilité stricte post-usage
La clé effective et les données sensibles sont stockées exclusivement en mémoire volatile et effacées immédiatement après usage. Cette volatilité constitue une limite structurelle contre la persistance involontaire.
Le zero-knowledge émergent repose sur l’absence ontologique de clé persistante et sur une composition entropique locale strictement volatile.
Principe d’émergence cryptographique
Formulation analytique
On peut désigner comme émergence cryptographique toute architecture dans laquelle un secret opérationnel ne possède pas d’existence persistante préalable, mais résulte d’une composition locale temporaire de composants cryptographiques autonomes.
Voir le schéma de reconstruction locale à clé segmentée : Zero-knowledge émergent non médié.
Dans ce modèle :
- Le secret effectif n’est pas stocké durablement.
- Il apparaît uniquement au moment de l’usage.
- Il disparaît immédiatement après l’opération.
Cette propriété distingue les architectures protégeant un secret préexistant des architectures produisant un secret temporaire par composition.
Hypothèses structurantes
L’émergence cryptographique suppose cumulativement :
- L’absence de clé maîtresse persistante.
- L’autonomie entropique des segments.
- Une reconstruction strictement locale.
- Une volatilité post-usage.
Conséquence informationnelle
Si l’on adopte un cadre shannonien, la robustesse maximale correspond à l’espace combinatoire résultant des entropies segmentaires mobilisées.
La sécurité devient alors fonction :
- De l’indépendance entropique des segments.
- De l’absence de secret global stocké.
- De la suppression de surface d’attaque persistante.
Formalisation minimale
Considérons un ensemble fini de segments cryptographiques autonomes :
Le nombre minimal de segments est fixé à deux (n ≥ 2), condition nécessaire pour qu’il y ait composition et non simple stockage. Toutefois, n n’est pas borné supérieurement.
Chaque segment Sᵢ est associé à une variable aléatoire indépendante Xᵢ possédant une entropie informationnelle H(Xᵢ).
La clé opérationnelle K est obtenue par une fonction de composition locale :
Dans le cas d’une concaténation contrôlée et sous hypothèse d’indépendance statistique :
La propriété d’émergence cryptographique peut alors être exprimée temporellement :
Autrement dit, la clé opérationnelle n’a pas d’existence persistante globale ; elle est instanciée exclusivement en mémoire volatile pendant une fenêtre d’usage Δt.
On distingue ainsi formellement :
- Les architectures à secret global persistant K₀,
- Des architectures à secret émergent K(t) défini uniquement pour t ∈ Δt.
Cette formalisation constitue une modélisation informationnelle minimale. Elle ne prétend pas démontrer une sécurité formelle complète, mais permet de caractériser analytiquement l’émergence cryptographique comme absence structurelle de secret persistant.
Attribution et origine conceptuelle
Le principe d’émergence cryptographique formulé ci-dessus trouve son origine dans l’invention de Jacques Gascuel, mise en œuvre dans le brevet international WO2018154258 et déployée au sein de plusieurs produits conçus et fabriqués par Freemindtronic. Cette invention repose sur une architecture de clés segmentées autonomes, sans serveur, sans base de données centralisée et sans clé maîtresse persistante. La formalisation doctrinale proposée dans cette chronique ne constitue pas un élément du brevet en tant que tel, mais une conceptualisation analytique a posteriori visant à qualifier le modèle dans le cadre plus large du débat sur le zero-knowledge en 2026. Autrement dit :
- L’architecture technique relève de l’invention de Jacques Gascuel.
- La formalisation en « principe d’émergence cryptographique » constitue une mise en perspective théorique de cette invention.
Cette précision permet de distinguer clairement :
- L’antériorité inventive (brevet),
- La formalisation doctrinale (analyse conceptuelle).
Positionnement méthodologique
La formalisation présentée ici constitue une analyse conceptuelle a posteriori d’une architecture existante. Elle vise à proposer un cadre d’interprétation dans le débat contemporain sur la gouvernance cryptographique.
Elle ne revendique pas un statut de théorie mathématique formellement démontrée, mais une structuration analytique destinée à clarifier les distinctions architecturales.
Discussion critique et limites
Toute formalisation doctrinale doit expliciter ses limites.
1 — Limite de validation formelle
Le principe d’émergence cryptographique constitue une grille analytique. Il ne remplace pas une preuve de sécurité formelle ni une démonstration mathématique complète au sens académique.
2 — Dépendance à l’implémentation
L’absence de clé persistante réduit certaines surfaces d’attaque, mais la robustesse effective dépend toujours :
- De la qualité entropique réelle des segments.
- De l’absence de fuite mémoire.
- De la résistance matérielle des dispositifs physiques.
3 — Hypothèse d’indépendance entropique
Le modèle suppose que les segments conservent une indépendance statistique suffisante. Toute corrélation non maîtrisée pourrait réduire l’espace combinatoire réel.
4 — Champ d’application
Le principe ne prétend pas s’appliquer universellement à toutes les architectures zero-knowledge. Il qualifie un sous-ensemble spécifique d’architectures compositionnelles non médiées.
Distinction avec les modèles cryptographiques classiques
Pour éviter toute confusion doctrinale, il convient de distinguer cette architecture des modèles existants.
- Shamir Secret Sharing : un secret préexistant est fragmenté. Ici, aucun secret maître persistant n’est découpé.
- HSM split key : une clé centrale existe et est protégée par fragmentation. Ici, la clé n’existe qu’au moment de l’usage.
- Multi-signature : validation distribuée par consensus. Ici, il n’existe ni réseau, ni validation distribuée.
- Zero-knowledge cloud : modèle médié par un fournisseur non détenteur. Ici, l’absence structurelle de tiers supprime la médiation.
Ainsi, le modèle relève d’une logique compositionnelle émergente et non d’un simple partage de secret.
Matrice de gouvernance cryptographique
Pour structurer l’analyse sans imposer une classification officielle, la matrice suivante isole les dimensions de gouvernance. Ainsi, elle clarifie où se situe l’autorité : dans la clé, dans les paramètres, dans la rétrocompatibilité, ou dans la transparence.
| Dimension | Question | Risque si faible | Irréversibilité |
|---|---|---|---|
| Possession de clé | Le fournisseur détient-il la clé ? | Rupture de confidentialité | Élevée |
| Gouvernance KDF | Qui fixe itérations et mémoire ? | Brute force facilité | Moyenne à élevée |
| Résistance au downgrade | Des modes faibles restent-ils acceptables ? | Dégradation forcée | Élevée |
| Origine de l’entropie | La source est-elle matériellement robuste ? | Secrets prédictibles | Critique |
| Agilité cryptographique | Migration ascendante maîtrisée ? | Obsolescence / rupture | Moyenne |
| Transparence | Plancher documenté publiquement ? | Opacité du modèle | Variable |
Typologie analytique (cadre d’analyse, non norme)
Enfin, pour qualifier les discours sans juger les acteurs, on peut utiliser une typologie analytique. Elle sert de grille, non de label. Ainsi, elle aide à comparer des architectures sans affirmer qu’une seule catégorie serait “la bonne”.
- Zero-knowledge déclaratif — non-possession de clé revendiquée, gouvernance paramétrique peu explicitée.
- Zero-knowledge négociable — paramètres ajustés par compatibilité, négociations possibles.
- Zero-knowledge à paramètres verrouillés — plancher cryptographique non négociable, refus explicite des modes faibles.
- Zero-knowledge souverain — contrôle utilisateur + invariance paramétrique + transparence, avec gouvernance clairement documentée.
Limites contemporaines et points d’arrêt
Lorsqu’un système laisse l’incertitude régner sur les paramètres, il crée une dette cryptographique. Par conséquent, la prudence impose un point d’arrêt : on ne scelle pas des données critiques sous des hypothèses fragiles. De plus, lorsque des paramètres faibles ont déjà servi, on doit envisager une migration complète plutôt qu’un simple “réglage”.
Limite humaine et gouvernance comportementale
Une architecture zero-knowledge peut être mathématiquement robuste et néanmoins fragilisée par des comportements humains inadéquats.
1 — Entropie comportementale insuffisante
Un mot de passe faible ou réutilisé réduit l’entropie effective, indépendamment des paramètres KDF.
2 — Sauvegarde non sécurisée
Exporter des secrets vers un support non protégé peut neutraliser les garanties architecturales.
3 — Mauvaise gestion des dispositifs physiques
Dans une architecture segmentée, la perte simultanée ou la conservation non maîtrisée de segments peut créer un risque opérationnel.
4 — Confusion entre simplicité et robustesse
La recherche d’ergonomie peut conduire à des compromis paramétriques.
Le zero-knowledge n’est pas uniquement une propriété cryptographique. Il constitue également une discipline comportementale.
Ainsi, la gouvernance cryptographique doit intégrer non seulement les paramètres techniques, mais aussi les usages réels et les pratiques humaines.
Références officielles (standards publics)
- RFC 8018 — PBKDF2 (PKCS #5)
- RFC 9106 — Argon2 Memory-Hard Function
- NIST SP 800-132 — Password-Based Key Derivation
- NIST — Random Bit Generation (SP 800-90 series)
- ISO/IEC 11770 — Key Management
- ENISA — Post-Quantum Cryptography & mitigation
- JACM — The Knowledge Complexity of Interactive Proof Systems
Bibliographie académique
- Shannon, C. E. (1948).
A Mathematical Theory of Communication.
Bell System Technical Journal, 27(3–4), 379–423, 623–656.
Lien officiel (archive Bell Labs / IEEE) :https://ieeexplore.ieee.org/document/6773024
- Goldwasser, S., Micali, S., & Rackoff, C. (1989).
The Knowledge Complexity of Interactive Proof Systems.
Journal of the ACM, 36(1), 97–115.
DOI officiel : https://doi.org/10.1145/28395.28420
- Krawczyk, H. (2010).
Cryptographic Extraction and Key Derivation: The HKDF Scheme.
Advances in Cryptology – CRYPTO 2010.
DOI Springer : https://doi.org/10.1007/978-3-642-14623-7_34
- Biryukov, A., Dinu, D., & Khovratovich, D. (2016).
Argon2: The Memory-Hard Function for Password Hashing and Other Applications.
IEEE European Symposium on Security and Privacy.
Version académique : https://doi.org/10.1109/EuroSP.2016.31
- ENISA (2023).
Post-Quantum Cryptography: Current State and Mitigation Strategies.
Publication officielle : https://www.enisa.europa.eu/publications/post-quantum-cryptography-current-state-and-quantum-mitigation
- NIST Special Publication 800-90A/B/C.
Recommendation for Random Bit Generators.
Références officielles NIST : https://csrc.nist.gov/projects/random-bit-generation
- ISO/IEC 11770.
Information technology — Security techniques — Key management.
Référence ISO officielle : https://www.iso.org/standard/63057.html
FAQ doctrinale
Zero-knowledge : ZKP et chiffrement côté client, c’est la même chose ?Définition
Deux concepts distincts
Non. Les ZKP décrivent une propriété de preuve sans divulgation. En revanche, le zero-knowledge de chiffrement décrit une architecture de confidentialité où le fournisseur ne détient pas la clé. Ainsi, les deux notions partagent un vocabulaire, mais elles ne décrivent pas le même objet.
Pourquoi la gouvernance des paramètres KDF devient-elle centrale ?Paramètres
Le plancher cryptographique définit la résistance
Parce que PBKDF2 et Argon2 dépendent d’itérations, de mémoire et d’un sel. Par conséquent, si ces paramètres sont négociables ou rétrocompatibles, la résistance au brute force peut baisser. Ainsi, la gouvernance des paramètres devient une condition de robustesse.
L’agilité cryptographique justifie-t-elle la négociation descendante ?Agilité
Agilité ≠ downgrade
Non. L’agilité organise une migration ascendante (post-quantique, modernisation). En revanche, le downgrade autorise une dégradation. Ainsi, même si l’agilité est nécessaire, elle ne doit pas ouvrir des chemins vers des paramètres faibles.
Pourquoi l’entropie est-elle une limite irréversible ?Entropie
La cryptographie dépend d’un phénomène physique
Parce que l’entropie détermine l’imprévisibilité. Ainsi, si la génération repose sur une source faible, augmenter les itérations plus tard ne reconstitue pas l’imprévisibilité initiale. Par conséquent, l’entropie constitue une frontière matérielle.
Glossaire
Zero-knowledge
Concept
Définition
Terme polysémique. Historiquement, il renvoie à une propriété de preuve (ZKP) où l’on démontre une assertion sans révéler le secret. En usage industriel, il désigne souvent un modèle de chiffrement côté client où le fournisseur ne détient pas la clé. En 2026, il implique aussi une gouvernance cryptographique : plancher non négociable, verrouillage du downgrade, paramètres KDF et entropie documentée.
Ancre interne : #zero-knowledge-definition
Zero-Knowledge Proofs (ZKP)
Preuve
Définition
Famille de protocoles permettant de prouver la validité d’une assertion sans divulguer l’information secrète. Les ZKP traitent de vérifiabilité et de non-divulgation, mais ne décrivent pas, à eux seuls, la gestion du cycle de vie des clés ni la gouvernance des paramètres.
Ancre interne : #zkp-definition
Gouvernance cryptographique
Doctrine
Définition
Ensemble des règles, responsabilités et mécanismes qui déterminent qui fixe les paramètres cryptographiques, comment ils évoluent, et ce qui est refusé (downgrade, modes hérités, paramètres faibles). Elle définit la robustesse effective plus sûrement qu’un slogan “sans clé côté fournisseur”.
Ancre interne : #gouvernance-cryptographique
Plancher cryptographique
Paramètres
Définition
Seuil minimal non négociable de paramètres (KDF, itérations, mémoire, longueurs de clés, politiques de refus, retrait des modes hérités). Il empêche qu’une architecture reste “zero-knowledge” nominalement tout en devenant fragile par compatibilité.
Ancre interne : #plancher-cryptographique
KDF (Key Derivation Function)
Dérivation
Définition
Fonction transformant un secret initial (mot de passe, matériau cryptographique) en clé exploitable. Les paramètres (itérations, mémoire, parallélisme, sel) conditionnent la résistance au brute force. Une gouvernance mature documente ces paramètres et interdit leur affaiblissement.
Ancre interne : #kdf-definition
Négociation descendante (downgrade)
Risque
Définition
Acceptation de paramètres plus faibles (ou d’algorithmes hérités) pour raisons de compatibilité. Même sans accès à la clé, un downgrade peut abaisser le plancher réel et créer une dette cryptographique difficile à corriger.
Ancre interne : #downgrade-definition
Agilité cryptographique
Migration
Définition
Capacité d’une architecture à migrer vers de nouveaux paramètres ou algorithmes sans rupture. L’agilité organise la montée en robustesse ; elle ne doit pas ouvrir des chemins de dégradation (downgrade).
Ancre interne : #agilite-cryptographique
entropie informationnelle (Shannon)
Mesure
Définition
Mesure mathématique de l’incertitude d’une source. En cryptographie, elle borne la sécurité maximale atteignable : un secret à faible entropie reste structurellement vulnérable, même avec un algorithme robuste ou un grand nombre d’itérations.
Ancre interne : #entropie-informationnelle
Entropie matérielle (hardware-rooted entropy)
Physique
Définition
Entropie issue de phénomènes physiques (TRNG/HRNG, bruit thermique, jitter). Elle renforce l’imprévisibilité à la génération. Une entropie insuffisante à la source crée une limite irréversible au niveau de sécurité.
Ancre interne : #entropie-materielle
Invariance paramétrique
Garantie
Définition
Propriété selon laquelle les paramètres critiques ne peuvent pas être réduits dynamiquement (par compatibilité, pression produit, ou interop legacy). Elle matérialise un plancher non négociable et rend le “zero-knowledge” plus robuste doctrinalement.
Ancre interne : #invariance-parametrique
principe d’émergence cryptographique
Architecture
Définition
Cadre analytique où la clé effective n’existe pas de manière persistante : elle émerge temporairement d’une composition locale de segments autonomes, puis est dissoute après usage. La sécurité dépend alors de l’autonomie entropique des segments et de l’absence de secret global stocké.
Ancre interne : #emergence-cryptographique
Cycle de vie des clés
Gestion
Définition
Ensemble des phases : génération, distribution, stockage, rotation, révocation et destruction. Une gouvernance zero-knowledge mature documente ces phases et identifie l’autorité responsable des décisions.
Ancre interne : #cycle-vie-cles
What We Didn’t Cover
Critère de qualification analytique
Pour qu’une architecture puisse être qualifiée de zero-knowledge en 2026, elle doit satisfaire cumulativement :
- Non-possession de clé par un tiers.
- plancher cryptographique documenté.
- Refus explicite du downgrade.
- Entropie mesurable à la génération.
- Gouvernance explicite du cycle de vie.
- Responsabilité clairement identifiable.
À défaut, le terme relève d’un usage déclaratif et non d’un régime de gouvernance.
Définition stabilisée du zero-knowledge en 2026
Afin d’éviter la confusion sémantique, on peut proposer une définition qualifiée :
Zero-knowledge (2026) désigne une architecture dans laquelle :
- Le fournisseur ne détient pas la clé de déchiffrement,
- Les paramètres cryptographiques disposent d’un plancher non négociable,
- Les chemins de downgrade sont explicitement verrouillés,
- L’entropie à la génération est mesurable et documentée,
- La gouvernance des clés est conforme aux standards publics.
Cette définition ne constitue pas une norme officielle. Elle propose un cadre d’analyse destiné à clarifier le débat.
Ainsi, le terme retrouve une précision conceptuelle adaptée aux exigences contemporaines.
Perspective stratégique : vers une maturité sémantique
Le zero-knowledge ne disparaît pas. Il évolue.
D’abord, il fut une propriété mathématique.
Ensuite, il devint un modèle de chiffrement côté client.
Aujourd’hui, il s’inscrit dans une gouvernance paramétrique.
Par conséquent, la maturité du débat exige une précision sémantique.
Si l’industrie souhaite préserver la confiance :
- Elle devra qualifier le terme au lieu de l’étendre indéfiniment.
- Elle devra publier les planchers cryptographiques.
- Elle devra verrouiller les rétrocompatibilités descendantes.
- Elle devra expliciter la qualité entropique à la génération.
En 2026, la cryptographie ne se limite plus aux algorithmes. Elle devient une discipline de gouvernance, de responsabilité et de limites irréversibles.
Le zero-knowledge ne se mesure plus au slogan. Il se mesure à l’invariance des paramètres.












